Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 백준 c++ 2468번
- c++
- 2870번 수학숙제
- 17070번
- Beakjoon
- 2870번 c++
- 프로그래머스
- 백준 1103번 게임
- 코테
- 백준 17070번 c++
- Unity
- 백준 1103번
- 2870번 수학숙제 c++
- 백준 2870번
- 2468 c++
- 수학숙제
- 코딩테스트
- 백준 1103번 c++
- 백준 17070번
- C#
- 플레이어 이동
- dfs
- 2870번
- Lv.3
- 백준
- Algorithm
- 오브젝트 풀링
- Lv2
- 백준 c++ 2870번
- 유니티
Archives
- Today
- Total
주녘공부일지
[Algorithm C#] 동적 계획법(DP) / Memoization, Tabulation 본문
1. 동적 계획법(DP : Dynamic Programming)
복잡한 하나의 큰 문제를 여러 개의 작은 문제로 나누어 해결하는 문제해결 방법 중 하나
- 작은 문제의 연산 결과를 저장해놓았다가 다시 큰 문제를 해결할 때 저장해둔 연산 결과를 다시 사용하는 문제해결 패러다임
즉, 메모리라는 공간 비용을 사용해 계산에 소요되는 시간 비용을 줄이는 방식
적용 조건
- 최적 부분 구조 : 작은 문제들의 연산 결과로 큰 문제의 답을 알 수 있는 구조
- 중복 부분 문제 : 작은 문제들의 연산은 중복된 연산으로 같은 값이 되는 문제
ex) 피보나치 수열, 등
+ Divide and Conquer(분할 정복)과의 차이점 : 중복되는 연산의 유무 ( 작은 문제의 답이 항상 같은가? )
2. 동적 계획법의 방식
| Top-Down (Memoization 방식) | 2) Bottom-Up (Tabulation 방식) |
| 큰 부분부터 작은부분으로 쪼개지며 답을 구함 - 문제 해결을 위해 필요한 부분만 연산 |
작은 부분부터 시작해 큰 부분까지 모두 답을 구함 - 모든 부분을 연산 |
| 재귀 함수로 구현되어 느림 (재귀, 반환) | 반복문으로 구현되어 빠름 (직접 액세스) |
| 모든 부분 연산을 수행하지 않아도 될 때 적합 | 모든 부분 연산을 수행해야 할 때 적합 |
| 너무 많은 연산 수행 시 스택 오버플로우 발생 |
ex) 피보나치 수열
피보나치 수 F(n)는 점화식으로 정의되는 수열
- F(1) = F(2) = 1
- F(n) = F(n-1) + F(n-2) // ( n > 1 )
// 편의에 따라 Dictionary<T>를 이용해도 무방
static int[] topDownMemoArray;
static int[] bottomupTableArray;
public static void Main()
{
int n = 30; // F(30)
topDownMemoArray = new int[n + 1];
bottomupTableArray = new int[n + 1];
topDownMemoArray[1] = 1;
bottomupTableArray[1] = 1;
Console.WriteLine($"BottomUp : {Fibo_BottomUp(n)}");
Console.WriteLine($"TopDown : {Fibo_TopDown(n)}");
}
// 재귀를 이용한 TopDown 구현 (Memoization 방식)
public static int Fibo_TopDown(int n)
{
if (n < 1)
return 0;
if (topDownMemoArray[n] == 0)
topDownMemoArray[n] = Fibo_TopDown(n - 1) + Fibo_TopDown(n - 2);
return topDownMemoArray[n];
}
// 반복문을 이용한 BottomUp 구현 (Tabulation 방식)
public static int Fibo_BottomUp(int n)
{
for (int i = 2; i <= n; i++)
if (bottomupTableArray[i] == 0)
bottomupTableArray[i] = bottomupTableArray[i - 1] + bottomupTableArray[i - 2];
return bottomupTableArray[n];
}(단, 피보나치 수열은 모든 부분 연산을 수행해야 하는 구조이므로 BottomUp 방식이 훨씬 유리함)
-> 얼마나 유리할까? ( 연산 성능 비교 )

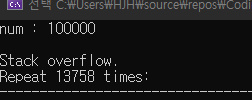
연산 성능 비교 코드
public static void Main()
{
int num = 10000; // 성능 비교 기준
bottomupTableArray = new int[n + 1];
topDownMemoArray = new int[n + 1];
bottomupTableArray[1] = 1;
topDownMemoArray[1] = 1;
Console.WriteLine($"num : {n}\n");
Stopwatch stopwatch = new Stopwatch();
// 재귀를 이용한 TopDown 연산
stopwatch.Start();
Fibo_TopDown(num);
stopwatch.Stop();
TimeSpan ts = stopwatch.Elapsed;
string elapsedTime = String.Format("{0:00}:{1:00}:{2:00}.{3:0000}",
ts.Hours, ts.Minutes, ts.Seconds, ts.Milliseconds);
Console.WriteLine("TopDown RunTime : " + elapsedTime);
stopwatch.Reset();
// 반복문을 이용한 BottomUp 연산
stopwatch.Start();
Fibo_BottomUp(num);
stopwatch.Stop();
ts = stopwatch.Elapsed;
elapsedTime = String.Format("{0:00}:{1:00}:{2:00}.{3:0000}",
ts.Hours, ts.Minutes, ts.Seconds, ts.Milliseconds);
Console.WriteLine("BottomUp RunTime : " + elapsedTime);
}'Programming > Algorithm' 카테고리의 다른 글
| [Algorithm C++] A* 알고리즘 ( Win32API ) (0) | 2024.09.28 |
|---|---|
| [Algorithm C#] 최소 신장 트리 MST ( 크루스칼, 프림 ) (1) | 2023.10.19 |
| [Algorithm C#] 소수 판별 최적화 알고리즘 (제곱근, 에라토스테네스의 체) (0) | 2023.08.25 |
| [Algorithm C#] BFS, DFS ( + Back Tracking ) (0) | 2023.03.09 |



